Linear Algebra (a primer)
Bruno Olshausen
Why linear algebra?
- What if more than one value is going in and coming
out of
a system? For example, we have many inputs coming into the retina
(photoreceptors)
and many outputs (retinal ganglion cells). Any single input affects
many
different outputs, and any given output is influenced by many different
inputs. How do we even begin to understand such a system?
- Linear algebra provides a useful tool for
characterizing
the behavior of systems where many values must be represented
simultaneously.
- e.g., the brain.
Vectors
- A vector is simply a list of numbers. A vector is
usually
denoted in boldface, or underlined:
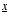 or
or 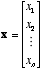 .
.
An “n-dimensional vector” has n elements.
One can think of
an n-dimensional vector as either a point in an n-dimensional
space, or as an arrow drawn from the origin to the point with
coordinates 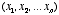 .
.
- The addition of two vectors is simply the addition of
their
elements:
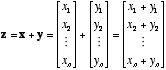 ,
,
Or, we could write the elements of z as 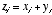 . Geometrically, vectors are added by placing them end to end. The
vector
from the origin to the tip of the last vector is the sum vector.
. Geometrically, vectors are added by placing them end to end. The
vector
from the origin to the tip of the last vector is the sum vector.
- The inner-product (or dot product)
of two vectors takes the sum of products of the elements of each
vector:
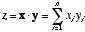 . This provides a measure of the similarity of two vectors (provided
you
know the length of each vector). If you divide the inner product by the
length of each vector, it gives you the cosine of the angle between them
. This provides a measure of the similarity of two vectors (provided
you
know the length of each vector). If you divide the inner product by the
length of each vector, it gives you the cosine of the angle between them
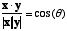
where 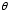 is the angle between the two
vectors, and
is the angle between the two
vectors, and 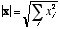 . An alternative geometric interpretation of the inner product is that
. An alternative geometric interpretation of the inner product is that 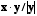 gives you the length of
gives you the length of  after it has
been projected onto y. Thus, orthogonal vectors have
an inner product of zero.The inner product is oftentimes also denoted
after it has
been projected onto y. Thus, orthogonal vectors have
an inner product of zero.The inner product is oftentimes also denoted 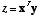 , where the superscript T denotes “transpose.” The
transpose of a
vector simply tilts it on its side so it is written as a row of
numbers,
, where the superscript T denotes “transpose.” The
transpose of a
vector simply tilts it on its side so it is written as a row of
numbers, 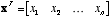 .
.
Matrices
- A matrix is just a 2D array of numbers. It is used to
map
a vector x into a new vector y via the relation
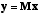 . It takes the place of the constant, k, in a simple one-dimensional
(scalar)
linear system. An m x n matrix M has elements
. It takes the place of the constant, k, in a simple one-dimensional
(scalar)
linear system. An m x n matrix M has elements
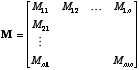
and we can write the resulting vector, y, elementwise as 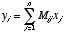 . In this case the vector y will be m-dimensional.
. In this case the vector y will be m-dimensional.
- Analysis/synthesis: the row vectors of a
matrix
tell you what part of the input space (vectors on the right side of the
matrix)
the matrix analyzes. The column vectors tell you what
part
of the output space (i.e., vectors coming out the left side) the matrix
can synthesize from any input. In each case, it is the number
of linearly independent vectors that define these spaces.
- Just as a linear scalar system can produce only a
limited
set of remappings of scalar values, so too is a matrix operation
limited
in the set of remappings it can produce. What do these remappings look
like? - rotations (orthonormal matrices) and scalings (diagonal
matrices) and
combinations thereof.
- If y=Mx and z=Ay, then z=AMx=Cx,
where C=AM is just another matrix. Thus, the
concatenation
of two matrix operations is just another matrix operation. The combined
matrix C is obtained via matrix multiplication:
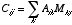
Note however that matrix multiplication is not commutative - i.e, 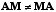 .
.
- Any matrix M can be decomposed in terms of a
rotation,
a scaling, and another rotation. i.e.,
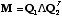 , where
, where 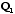 and
and 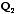 are orthonormal matrices
(rotation) and
are orthonormal matrices
(rotation) and 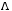 is a diagonal matrix
(scaling).
is a diagonal matrix
(scaling).
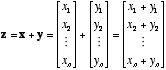 ,
, 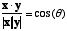
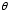 is the angle between the two
vectors, and
is the angle between the two
vectors, and  after it has
been projected onto y. Thus, orthogonal vectors have
an inner product of zero.The inner product is oftentimes also denoted
after it has
been projected onto y. Thus, orthogonal vectors have
an inner product of zero.The inner product is oftentimes also denoted 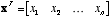 .
. 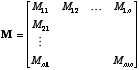
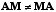 .
. is a diagonal matrix
(scaling).
is a diagonal matrix
(scaling).